
| Research, Patent, Publications, Grants, and Graduate Students | Water Chemistry Data |

Ron was born in 1947 in New Orleans, Louisiana, and grew up in the rice country in Southwest Louisiana. He received his B.S. in Geology in 1968 from LSU and then went to northern Guatemala to do field geology that summer. While doing field work he had the interesting experience of being captured by Indians, held for a trial on tribal lands, and then released with an ear of corn as a token of friendship. (Never underestimate a "drunken but determined group" of pygmy Mayan Indians with machetes and ropes!) In the fall of 1968, he started graduate school at Penn State University but - under threat of being drafted - enlisted for two years in the US Army and served in the mechanized infantry until 1970. To his eternal gratitude, the Army sent him to Germany and not to Viet Nam. After his discharge, Ron went back to LSU in 1971 and received his M.S. in Geology in 1974. At LSU, he worked with Jeff Hanor and measured diffusion coefficients of cations in multi-salt solutions within an artificial porous media. (Why work with real rocks when you can make your own!) Ron left LSU in 1973 for graduate work at UC Berkeley where he received his Ph.D. in 1977. He worked with Harold Helgeson doing a combined field and laboratory study of the geochemical origin of sepiolite at Sinya, Kenya, determining the thermodynamic properties of the mineral. Richard Hay, the Berkeley field geologist at Olduvai Gorge and Richard Leaky, the Kenyan paleontologist, were his field supervisor and sponsor in Africa. Ron had married Louise Poorman Baenninger, an experimental psychologist from Johns Hopkins in 1974 and they spent the summer of 1975 at Ol Tukai in Amboseli National Park on the Tanzania border, doing his field work at Sinya on the northern edge of Mt. Kilimanajaro. It was an incredible summer!
As an undergraduate and before going to graduate school at LSU, Ron worked as an exploration geologist for Union Oil of California in Lafayette, Louisiana. After graduate school at Berkeley, he moved to Houston in 1977, working for a year as a Research Geologist in Exxon Production Research Company. He began his academic career in 1978 at his alma mata LSU as an Assistant Professor on soft money in Coastal Studies at LSU. He joined UNO in 1982, becoming an Associate Professor in 1984, a Professor in 1990, and a Research Professor in 2004. Ron's research interests are in low-temperature geochemistry applied to environmental problems. He has been accused of being a resort geochemist because of his many years of research of the mixing zone along the Caribbean Sea in the Yucatan. After Hurricane Karina devastated New Orleans in 2005, he set up a mobile chemical laboratory for doing water chemistry (Chemistry on Wheels or COW) in the field on his research projects.
Ron retired at the end of the 2006 fall semester but continued his research as Professor Emeritus at UNO. He splits time between Louisiana and North Carolina. Following Hurricanes Katrina and Rita in 2005, he and his second wife (Londi Moore) bought a house on a ridge west of Murphy, North Carolina, where he looked into the ground-water chemistry within crystalline rocks and overlying soils of the Appalachian Mountains.
Ron and Londi did two nature-friendly residential developments: Square 74 and Old Mandeville Woods in Louisiana. Preserving wildlife habitat was important to them. They were both active in animal sanctuaries, shelters, and rescues, funding the spay and neuter program in the City of Mandeville for several years and helping to fund St. Francis Animal Sanctuary in Tylertown, Mississippi, for the North Shore area of the Florida Parishes. In North Carolina in 2006 and 2007 they began the nature-friendly residential subdivison Cameron's Ridge which was mothballed in 2008 due to the recession and is still inactive, waiting for the development to be finished by David due to Ron's lack of energy. In 2008 Londi, acting as the unpaid Volunteer Shelter Director, and Ron helped fund the evolution of a low-kill Animal Shelter the Valley River Humane Society (VRHS) Shelter in Murphy, North Carolina, for Cherokee and adjacent counties. Much of that effort was over-turned in 2009 by local politics in the county - never underestimate PETA's desire to euthanize stray dogs and cats contrary to their efforts to save wildlife. In March, 2009, Ron incorporated Logan's Run Rescue (LRR), forming it with Londi for doing rescue work and spay and neuter in SW North Carolina and adjacent areas in Georgia and Tennessee. The rescue is named after Logan who died tragically on July 17, 2008. Londi decided that life in North Carolina was not to be and moved back to Mandeville, Louisiana in 2010, initialing serving as unpaid Director of St Francis Animal Sanctuary. Meanwhile, Ron stayed in North Carolina and Logans Run Rescue became very successful. However, in a nasty political power struggle, typical of 501(c)(3) rescues, LRR was taken over in 2012 by the Board who dismantled most of the rescue work to concentrate on spay and neuter. Interestingly enough, at this same time Londi ran adrift of politics at St Francis Animal Sanctuary and resigned from her job. We painfully learned there are alway a few people working in Animal Rescues who will use the Rescues to further their own interests and their supporters can either be oblivious to what is happening or do not care.
Ron then began working with Casey Lattimer, President of The Delta Humane Society of Louisiana (DHS) in Rayville, Louisiana. Casey would ship rescue dogs from Murphy, North Carolina to northeast rescues during her DHS transports from Louisiana. In 2014, he formed a new 501(c)(3) rescue, Lost Dogs Run (LDR) in North Carolina with the help of his friend Melissa Marcum and his son David. Cindy Mulkey now helps with the rescue and serves as its vice president. LDR promotes fostering for unwanted animals nation-wide. Please help support your local rescue, sanctuary, and humane societies.
In 2014, Ron built a small cabin (The Howling Wolf Cabin) on a mountain spur in the center of 50 acres of woods (The Little Easy). The mountain is Fort Butler Mountain, the infamous starting point for the Cherokee Trail of Tears. He has several acres of fenced yards that lead back through doggy doors into the cabin. Here he lives with his pack of rescue dogs, running Lost Dogs Run with Cindy Mulkey, hiking with Cindy in the mountains and looking for gems in "all the wrong places" while reflecting on his life.
| Ron has one child, David Stoessell, born in 1976 in Berkeley, whose mother was Louise Baenninger, Ron's first wife. Louise and Ron were divorced in 1991, but have kept in close contact. After 4 years in the US Air Force, David received his B.S. in 2003, in Architectural Engineering from the University of Texas in Austin. In 2010, he received his PE license and a M.B.A. in real estate development from Arizona State University in Phoenix. David's first wife was to TV anchor Isis Romero and he is now married to Shelly Mosing, a Louisiana girl from Luling. They live in the Austin hills and he does engineering evaluations of properties nationwide for clients with occasional real estate projects in Texas and Louisiana. | Ron married Yolanda (Londi) Moore in 1991, a geohydrologist with a M.S. in Geology from UNO. Londi built houses with a passion for design. She and Ron have developed subdivisions that are environmentally friendly with wildlife servitudes and lots of green space, see Old Mandeville Woods, Cameron's Ridge, and Square 74. She also holds a North Carolina contractor's license. They separated in 2010 but remain good friends and look after each other's interests. Before their separation, they had moved to Murphy, North Carolina. Londi went back to Mandeville, Louisiana and now lives in a house she built in a wooded square near Old Mandeville Woods. | In Louisiana, Ron and Londi lived in the Teal Tree House on Lake Pontchartrain in Mandeville with their rascals: two Cavalier spaniels - grumpy Cameron and saintly Logan - and with foxy Josey, una perrita de las calles de San Ramon de Costa Rica. Can you tell which is which below? Logan died tragically in 2008 and Cameron passed from heart problems in 2010. While in retirement in North Carolina, in 2014 Ron built and now lives in the Howling Wolf Cabin on 50 acres named The Little Easy on the slopes of Fort Butler Mountain. Logan and Cameron are buried there at Standing Rock along with lost dogs of Lost Dogs Run. Cindy White Mulkey in Murphy, is his companion, a good friend who keeps him sane. |
 Now listen Up! Cameron taking charge in 2001  David and Isis (2006) 
Beginning of David's Development in 2007 |
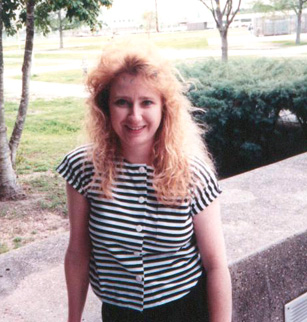 Londi as a UNO M.S. graduate student in 1990  Londi doing Yucatan hydrology in 1991  Entrance to Old Mandeville Woods (2005) "Our 1st development" |

The Teal Tree House by Terrance Osborne (2006)  The Rascals by Leah Stanley (2004)  Winter Blue Ridge View from our North Carolina deck |
For 25 years Ron did research in the Yucatan and along the Caribbean coast. In his last study in 2004, Ron and Jim Coke, a well-known cave diver in the Yucatan, sampled some of the deep interior sinkholes. The jungle terrain and beautiful sinkholes made this an incredible place to do a study. The goals included explaining the origin of this water which begins as seawater and ends up being modified by evaporite dissolution under the Yucatan interior. The overlying fresh water composition is controlled by mixing due to thermal convection from heat transfer upward from the warm saline water into the cooler fresh water, producing a uniform brackish composition with depth, see
Stoessell and Coke, 2006.
Other projects for other researchers to work on in the Yucatan include determining the rates of calcite raft formation at the water surface in caves due to degasing of carbon dioxide, finding more examples of heat anomalies in the cenote haloclines that are thought to be due to local geothermal convection cells, see Stoessell et al., 2002, and measuring flow rates in the underlying saline water. See Ron's list of journal publications ("Publications) for those related to the Yucatan.
In Louisiana, prior to retirement, Ron was working on the origin of near-surface brackish waters that contaminate fresh water aquifers in South Louisiana, e.g., the Baton Rouge fresh-water aquifers and those of SE and SW Louisiana. He used geochemical fingerprint techniques, previously used in Central Louisiana to pinpoint salt sources in the Mississippi River River Alluvium Aquifer Stoessell (1997). The new investigation showed the source of the salt (see Stoessell and Prochaska (2005)) is from brines in deeper aquifers moving updip on the fault plane of east-west trending faults and then into the freshwater aquifers. The Baton Rouge USGS has opposed this view, arguing that "in situ" marine saltwater in deeper parts of the near-surface aquifers is simply moving updip within the aquifers and crossing the faults. This kind of detective research is crucial in understanding the movement of subsurface fluids and hopefully will be continued by other researchers.
| Research Experience | Patent & PDF Copies of Signficant Publications & a List of Abstracts |
Grants Received | Graduate Students |
In anticipation of retirement, Ron starting putting water compositional data on this web site. These are data that he has collected in various projects over the years. The analytical methods are described in the publications which are mentioned in the files. Some of the data are unpublished and some are from student MS thesis projects that he supervised. Please email Ron for instructions as to how to reference the data if you want to use it in a publication or for other public use.
|
Amboseli, Kenya PDF file |
Barbados PDF File |
South Louisiana PDF File |
Southwest North Carolina PDF File |
Yucatan PDF File |

Pilated woodpecker on a cypress tree behind the teal tree house (3/11/06)